
Zadanie Tanie podróże (tan)
Pomóż nam usprawnić bazę zadań!
Tanie podróże
Limit pamięci: 32 MB
Pasażerowie autokarów turystycznych, przewożących wycieczki transkontynentalną autostradą,
spędzają w drodze wiele dni, zatem opłaty za noclegi stanowią poważną część kosztów podróży.
Ze względu na bezpieczeństwo jazdy i wygodę pasażerów każdy autokar jedzie tylko w ciągu dnia i nie może przejechać więcej niż 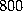 km dziennie.
Noce na trasie (poza jej początkiem i końcem) pasażerowie i kierowca spędzają w hotelach.
km dziennie.
Noce na trasie (poza jej początkiem i końcem) pasażerowie i kierowca spędzają w hotelach.
Dotychczas planowano przejazdy tak, by liczba noclegów na trasie była jak najmniejsza. Dążąc do obniżki kosztów, przedsiębiorstwo przewozowe zdecydowało zbadać, czy opłaci się układanie planów podróży tak, by suma opłat za noclegi była możliwie najniższa, nawet gdyby to miało przedłużyć podróż. W tych obliczeniach można korzystać z ofert hoteli położonych przy autostradzie. W każdej ofercie jest podana odległość hotelu od początku trasy i cena jednego noclegu jednej osoby.
Podróż jest tylko w jedną stronę. Trasa nie ma rozgałęzień. Przez każdy punkt trasy autokar przejeżdża jeden raz. Nigdzie na trasie nie ma dwóch hoteli w jednym punkcie, więc dla zidentyfikowania hotelu wystarczy podać jego odległość od początku trasy. Nie planuje się noclegu na początku ani na końcu trasy. Liczba osób w autobusie nie zmienia się i w każdym hotelu wszyscy (łącznie z kierowcą) płacą za nocleg jednakowo — zgodnie z ofertą. Pojemność hoteli jest na tyle duża, że nie istnieje problem braku miejsc. Zawsze można liczyć na to, że w dowolnej chwili w każdym hotelu będzie wystarczająco dużo wolnych miejsc, by przenocować wszystkich pasażerów autobusu.
Na każdym odcinku trasy o długości 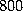 km jest przynajmniej jeden hotel, co oznacza, że przejechanie trasy z zachowaniem podanych wyżej warunków jest możliwe.
km jest przynajmniej jeden hotel, co oznacza, że przejechanie trasy z zachowaniem podanych wyżej warunków jest możliwe.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia dane: długość trasy, liczbę hoteli oraz oferty hoteli;
- znajduje dwa plany podróży:
- najtańszej, tzn. takiej, żeby suma opłat za hotele była najmniejsza, a jeśli takich rozwiązań jest wiele, wybiera jedno z najmniejszą liczbą noclegów,
- najszybszej, tzn. takiej, żeby liczba noclegów była najmniejsza, a jeśli takich rozwiązań jest wiele, wybiera jedno z najmniejszą sumą opłat za noclegi;
- zapisuje wyniki, tj. dwa plany podróży — najtańszej i najszybszej, na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia są zapisane dwie liczby całkowite dodatnie,
oddzielone pojedynczym odstępem: długość trasy  w kilometrach oraz liczba hoteli
w kilometrach oraz liczba hoteli 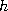 ,
gdzie
,
gdzie 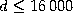 i
i 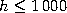 .
.
W kolejnych 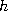 wierszach są zapisane oferty hoteli — każda oferta w osobnym wierszu.
Są one uporządkowane według rosnącej odległości hoteli od początku trasy.
Każda oferta jest zapisana w postaci dwóch liczb całkowitych dodatnich oddzielonych pojedynczym odstępem, pierwsza liczba —
to odległość hotelu od początku trasy w kilometrach, a druga — to cena jednego noclegu w tym hotelu nie większa niż
wierszach są zapisane oferty hoteli — każda oferta w osobnym wierszu.
Są one uporządkowane według rosnącej odległości hoteli od początku trasy.
Każda oferta jest zapisana w postaci dwóch liczb całkowitych dodatnich oddzielonych pojedynczym odstępem, pierwsza liczba —
to odległość hotelu od początku trasy w kilometrach, a druga — to cena jednego noclegu w tym hotelu nie większa niż 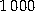 .
.
Wyjście
W pierwszym wierszu standardowego wyjścia należy zapisać plan podróży najtańszej — odległości kolejnych miejsc noclegu od początku trasy. W drugim wierszu należy — w taki sam sposób — zapisać plan podróży najszybszej. Liczby w wierszu powinny być pooddzielane pojedynczym odstępem.
Przykład
Dla danych wejściowych:
2000 7 100 54 120 70 400 17 700 38 1000 25 1200 18 1440 40
poprawną odpowiedzią jest:
400 1200 400 1200
Autor zadania: Stanisław Waligórski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English